The Unit 4 Congruent Triangles Test delves into the fundamental concepts and applications of triangle congruence, providing students with a comprehensive evaluation of their understanding. This assessment encompasses the essential criteria, methods, and applications of triangle congruence, ensuring a thorough examination of this critical geometric concept.
Throughout the test, students will demonstrate their proficiency in identifying and proving congruent triangles, utilizing the SSS, SAS, and AAS criteria. They will apply their knowledge to solve problems involving angle measurement, side length calculation, and area and perimeter determination, showcasing their ability to apply triangle congruence in practical scenarios.
Congruent Triangles Overview
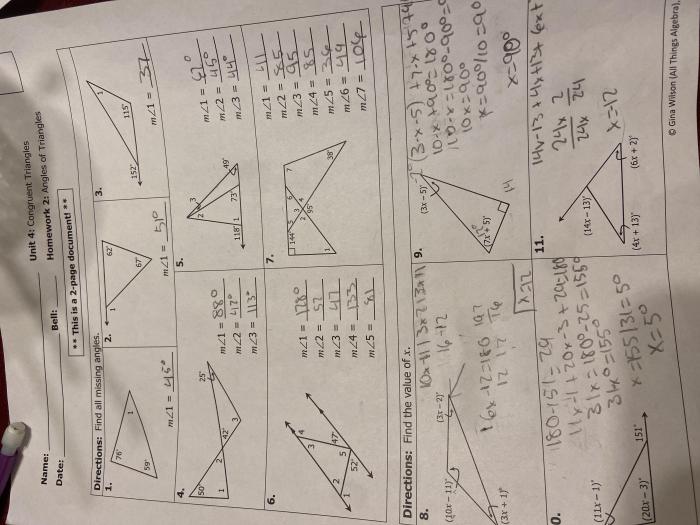
In geometry, congruent triangles are triangles that have the same shape and size. This means that they have the same three side lengths and the same three angles.
Congruent triangles are often used in architecture, engineering, and other fields where precision is important. For example, architects use congruent triangles to design buildings that are structurally sound, and engineers use congruent triangles to design bridges that can withstand heavy loads.
Properties of Congruent Triangles
Congruent triangles have a number of properties, including the following:
- Their corresponding sides are equal in length.
- Their corresponding angles are equal in measure.
- Their areas are equal.
- Their perimeters are equal.
Criteria for Congruency
Determining whether two triangles are congruent is crucial in geometry. Congruent triangles are those that have the same size and shape. To establish congruence, specific criteria must be met. These criteria, known as SSS, SAS, and AAS, provide the necessary conditions to ensure that two triangles are congruent.
The SSS (Side-Side-Side) criterion states that if the corresponding sides of two triangles are equal in length, then the triangles are congruent. For example, if triangle ABC has sides of length 3 cm, 4 cm, and 5 cm, and triangle XYZ has sides of length 3 cm, 4 cm, and 5 cm, then triangles ABC and XYZ are congruent by the SSS criterion.
The SAS (Side-Angle-Side) criterion states that if two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, then the triangles are congruent. For example, if triangle ABC has sides AB and BC of length 3 cm and 4 cm, respectively, and angle B is 60 degrees, and triangle XYZ has sides XY and YZ of length 3 cm and 4 cm, respectively, and angle Y is 60 degrees, then triangles ABC and XYZ are congruent by the SAS criterion.
The AAS (Angle-Angle-Side) criterion states that if two angles and the included side of one triangle are equal to two angles and the included side of another triangle, then the triangles are congruent. For example, if triangle ABC has angles A and B of 60 degrees and 30 degrees, respectively, and side AB is 3 cm, and triangle XYZ has angles X and Y of 60 degrees and 30 degrees, respectively, and side XY is 3 cm, then triangles ABC and XYZ are congruent by the AAS criterion.
| Criteria | Description | Example |
|---|---|---|
| SSS | Corresponding sides are equal in length | Triangle ABC with sides 3 cm, 4 cm, 5 cm is congruent to triangle XYZ with sides 3 cm, 4 cm, 5 cm |
| SAS | Two sides and the included angle are equal | Triangle ABC with sides AB and BC of length 3 cm and 4 cm, and angle B of 60 degrees is congruent to triangle XYZ with sides XY and YZ of length 3 cm and 4 cm, and angle Y of 60 degrees |
| AAS | Two angles and the included side are equal | Triangle ABC with angles A and B of 60 degrees and 30 degrees, and side AB of length 3 cm is congruent to triangle XYZ with angles X and Y of 60 degrees and 30 degrees, and side XY of length 3 cm |
Proving Triangle Congruency
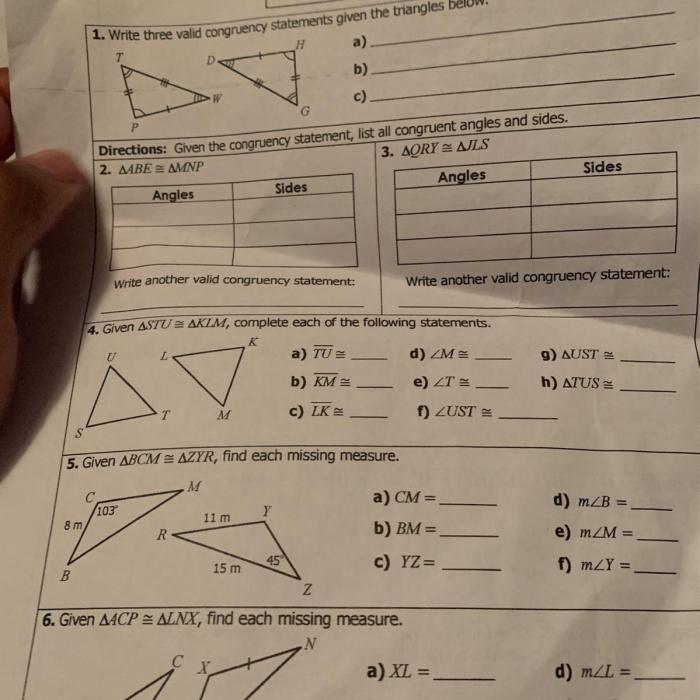
Establishing triangle congruency requires adherence to specific criteria. To demonstrate the process, we will delve into the steps involved and provide a detailed example.
Steps Involved in Proving Triangle Congruency
- Identify the given information:Determine the known measurements and relationships within the triangles.
- Apply the relevant congruence criteria:Select the appropriate criterion based on the available information (SSS, SAS, ASA, AAS, or HL).
- State the congruence property:Express the specific rule that justifies the triangles’ congruency.
Example: Proving Triangle Congruency Using SAS
Given:Triangle ABC with AB = 5 cm, BC = 7 cm, and ∠B = 45°. Triangle DEF with DE = 5 cm, EF = 7 cm, and ∠E = 45°.
To Prove:ΔABC ≅ ΔDEF
Proof:
- Given:AB = 5 cm, BC = 7 cm, ∠B = 45°, DE = 5 cm, EF = 7 cm, and ∠E = 45°.
- Apply the SAS Congruence Criterion:Since AB = DE, BC = EF, and ∠B = ∠E, we can apply the SAS Congruence Criterion.
- State the Congruence Property:By SAS Congruence Criterion, ΔABC ≅ ΔDEF.
Applications of Congruency
Triangle congruency finds widespread applications in various branches of geometry, enabling us to solve complex problems related to angle measurement, side length calculation, and area and perimeter determination.
Angle Measurement
Congruent triangles possess equal corresponding angles. By identifying congruent triangles within geometric figures, we can determine unknown angle measures. For instance, if two triangles share a common side and the other two sides are congruent, the angles opposite the congruent sides are also congruent.
Side Length Calculation
Triangle congruency allows us to find unknown side lengths. If two triangles are congruent, their corresponding sides are equal in length. By establishing congruence between triangles, we can utilize known side lengths to determine the lengths of unknown sides.
Area and Perimeter Determination, Unit 4 congruent triangles test
The areas and perimeters of congruent triangles are equal. By determining the area or perimeter of one congruent triangle, we can directly obtain the corresponding values for the other congruent triangles. This principle is particularly useful in calculating the areas and perimeters of complex geometric shapes composed of congruent triangles.
Practice Problems: Unit 4 Congruent Triangles Test
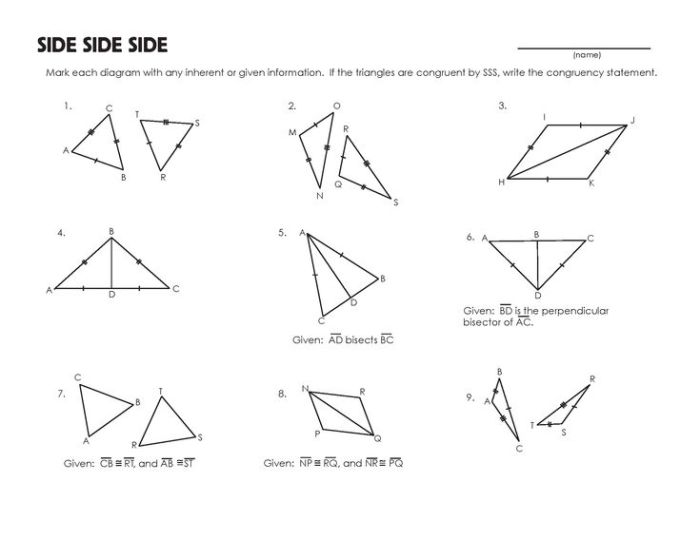
Practice problems are essential for students to solidify their understanding of triangle congruency. These problems allow students to apply the criteria for congruency and develop their problem-solving skills.
The following set of practice problems is designed to cater to different skill levels. Some problems are straightforward, while others require more complex reasoning and application of multiple criteria.
Sample Problems
- Given two triangles with two pairs of congruent sides, prove that the triangles are congruent.
- Prove that two triangles are congruent if they have one pair of congruent angles and the included sides are congruent.
- Determine whether the following triangles are congruent. If they are, state the criterion for congruency used.
- Triangle ABC: AB = 5 cm, BC = 4 cm, CA = 3 cm
- Triangle DEF: DE = 5 cm, EF = 4 cm, DF = 3 cm
Common Errors and Misconceptions
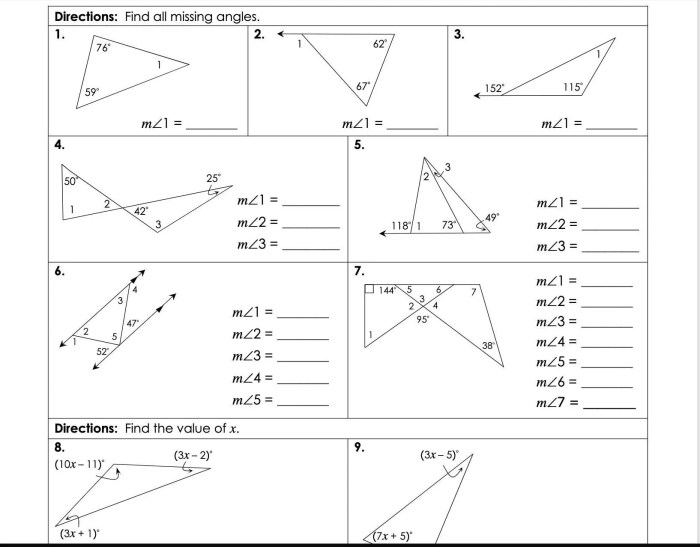
In dealing with triangle congruency, students often encounter errors and misconceptions. These can hinder their understanding of the concept and its applications. It is crucial to identify and address these misconceptions to ensure a thorough understanding of triangle congruency.
Misconception: All congruent triangles are identical
This is a common misconception. While congruent triangles have the same shape and size, they may not be identical in terms of orientation or placement. They can be rotated or flipped, resulting in different orientations.
Misconception: Congruency implies equality of all corresponding parts
While congruent triangles have corresponding parts that are equal in length or measure, it is essential to note that this equality applies only to corresponding parts. For instance, if two triangles are congruent based on the SSS criterion, it means their corresponding sides are equal, but their corresponding angles may not necessarily be equal.
Misconception: The SAS Congruency Theorem is valid for all triangles
The SAS Congruency Theorem is only valid when the included angle is not the largest angle in the triangle. If the included angle is the largest angle, the theorem does not apply, and other criteria for congruency should be considered.
Technology Integration
Technology can significantly enhance the teaching and learning of triangle congruency by providing interactive and engaging experiences.
One of the most effective ways to use technology in this context is through interactive simulations. These simulations allow students to manipulate triangles, explore different transformations, and observe the effects on congruency in real-time. For example, the “Triangle Congruency Simulator” from GeoGebra allows students to create and move triangles, measure their sides and angles, and observe the impact on their congruence.
Online Tools and Apps
Numerous online tools and apps are available to support the teaching and learning of triangle congruency. These tools often provide interactive exercises, quizzes, and games that make learning more engaging and fun.
- The “Triangle Congruency Practice” app from Mathway offers a variety of exercises on different types of triangle congruency, with step-by-step solutions.
- The “Congruent Triangles” game from Sheppard Software provides a game-like environment where students can match congruent triangles and earn points for correct answers.
Quick FAQs
What are the three criteria for determining triangle congruence?
The three criteria for determining triangle congruence are Side-Side-Side (SSS), Side-Angle-Side (SAS), and Angle-Angle-Side (AAS).
How can I prove that two triangles are congruent using the SSS criterion?
To prove that two triangles are congruent using the SSS criterion, you need to show that all three sides of one triangle are equal to the corresponding three sides of the other triangle.
What are some common applications of triangle congruence?
Triangle congruence has many applications in geometry, including solving problems related to angle measurement, side length calculation, and area and perimeter determination.