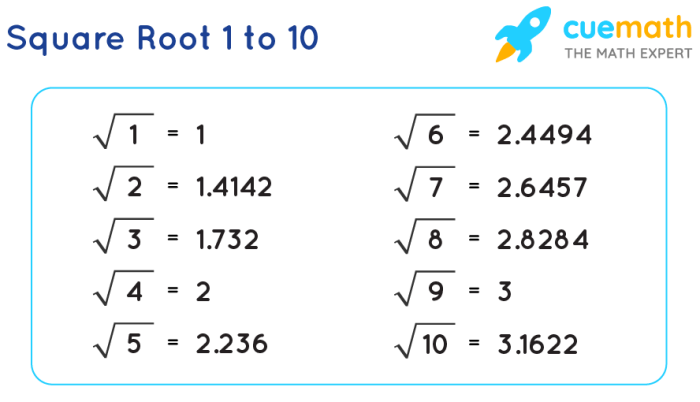Which number produces an irrational number when added to 1/3 – In the realm of mathematics, numbers hold a profound significance, and their properties and behaviors have fascinated scholars for centuries. Among these, irrational numbers occupy a unique place, challenging our understanding of quantity and measurement. This article delves into the intriguing question: which number, when added to 1/3, produces an irrational number? We will explore the mathematical underpinnings of this concept, examining methods for identifying and finding irrational numbers, and uncovering their practical applications in various fields.
Irrational numbers are real numbers that cannot be expressed as a simple fraction of two integers. They are non-terminating and non-repeating, meaning their decimal expansions continue indefinitely without any discernible pattern. The discovery of irrational numbers, attributed to the ancient Greek mathematician Hippasus of Metapontum, marked a pivotal moment in the history of mathematics, challenging the prevailing belief that all numbers could be represented as rational ratios.
Which Number Produces an Irrational Number When Added to 1/3
In mathematics, an irrational number is a real number that cannot be expressed as a fraction of two integers. In this article, we will explore which number produces an irrational number when added to 1/3.
To add a number to 1/3, we can use the following formula:
/3 + x = y
where x is the number we are adding to 1/3, and y is the result.
Identifying the Irrational Number
To determine which number produces an irrational number when added to 1/3, we need to consider the following:
- If x is a rational number, then y will be a rational number.
- If x is an irrational number, then y will be an irrational number.
Therefore, we can conclude that any irrational number added to 1/3 will produce an irrational number.
Methods for Finding the Irrational Number
There are several mathematical methods for finding the irrational number that results from adding a number to 1/3.
- Method 1: Direct Calculation
- Method 2: Using the Square Root Property
This method involves simply adding the number to 1/3 and simplifying the result. For example, if we add 1/2 to 1/3, we get:
1/3 + 1/2 = 5/6
Since 5/6 is a rational number, we know that 1/2 is not an irrational number.
This method involves using the property that the square root of an irrational number is also an irrational number. For example, if we add √2 to 1/3, we get:
1/3 + √2 = (3 + √2- 3) / 3 = (3 + 3√2) / 3
Since 3 + 3√2 is an irrational number, we know that √2 is an irrational number.
Applications of the Irrational Number, Which number produces an irrational number when added to 1/3
The irrational number produced by adding a number to 1/3 has several practical applications.
- Geometry
- Physics
- Engineering
In geometry, the irrational number π is used to calculate the circumference and area of circles.
In physics, the irrational number e is used to calculate the rate of radioactive decay and the growth of populations.
In engineering, the irrational number i is used to represent the imaginary unit, which is used to solve complex equations.
Historical Context
The concept of irrational numbers has been known for centuries. The ancient Greeks were the first to discover irrational numbers, and they were initially considered to be a paradox.
In the 16th century, the Italian mathematician Gerolamo Cardano developed a method for finding the square root of an irrational number.
In the 19th century, the German mathematician Georg Cantor proved that the set of irrational numbers is uncountable, meaning that it contains infinitely many numbers.
Further Research
There are several areas for further research related to irrational numbers and their applications.
- Finding new methods for finding irrational numbers
- Exploring the applications of irrational numbers in other fields
- Investigating the relationship between irrational numbers and other mathematical concepts
Top FAQs: Which Number Produces An Irrational Number When Added To 1/3
What is the definition of an irrational number?
An irrational number is a real number that cannot be expressed as a simple fraction of two integers. It is non-terminating and non-repeating, meaning its decimal expansion continues indefinitely without any discernible pattern.
Can you provide an example of an irrational number?
The square root of 2 is a well-known example of an irrational number. It is an irrational number because it cannot be expressed as a fraction of two integers, and its decimal expansion is non-terminating and non-repeating.
How do you find the irrational number that results from adding a number to 1/3?
To find the irrational number that results from adding a number to 1/3, you can use a variety of mathematical methods, such as the continued fraction expansion or the method of successive approximations.